Method 2: Using a table of critical values. The two methods are equivalent and give the same result. There are two methods of making the decision. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between x and y in the population. Alternate Hypothesis H a: The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS NOT a significant linear relationship(correlation) between x and y in the population. Null Hypothesis H 0: The population correlation coefficient IS NOT significantly different from zero. If r is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed x values in the data. If r is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction. If r is significant and the scatter plot shows a linear trend, the line can be used to predict the value of y for values of x that are within the domain of observed x values. Therefore, we CANNOT use the regression line to model a linear relationship between x and y in the population. X and y because the correlation coefficient is not significantly different from zero.” What the conclusion means: There is not a significant linear relationship between x and y. 
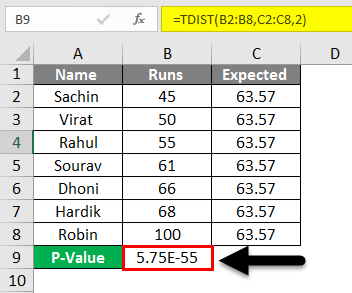
If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that correlation coefficient is “not significant.”Ĭonclusion: “There is insufficient evidence to conclude that there is a significant linear relationship between We can use the regression line to model the linear relationship between x and y in the population. What the conclusion means: There is a significant linear relationship between x and y. If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is “significant.”Ĭonclusion: There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero. We decide this based on the sample correlation coefficient r and the sample size n. Ρ is “close to zero” or “significantly different from zero”. The hypothesis test lets us decide whether the value of the population correlation coefficient
r = sample correlation coefficient (known calculated from sample data). 
ρ = population correlation coefficient (unknown). The symbol for the population correlation coefficient is ρ, the Greek letter “rho.”. The sample correlation coefficient, r, is our estimate of the unknown population correlation coefficient. But because we have only have sample data, we cannot calculate the population correlation coefficient. If we had data for the entire population, we could find the population correlation coefficient. The sample data are used to compute r, the correlation coefficient for the sample. We perform a hypothesis test of the “ significance of the correlation coefficient” to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population. We need to look at both the value of the correlation coefficient r and the sample size n, together. However, the reliability of the linear model also depends on how many observed data points are in the sample. The correlation coefficient, r, tells us about the strength and direction of the linear relationship between x and y. 
Calculate and interpret the correlation coefficient.
0 kommentar(er)
